完全二叉树的应用 — 堆
目录
堆
堆是一种特殊的完全二叉树,只有最小堆和最大堆。
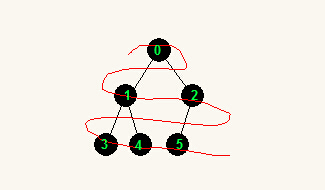
最小堆:完全二叉树中,父结点都不大于(<=)子结点。最小堆的根结点是最小的。
最大堆:完全二叉树中,父结点都不小于(>=)子结点。最大堆的根结点是最大的。
最小堆的子树也是最小堆,同理,最大堆的子树也是最大堆。
像上面的图,根结点是最小的,且所有父结点都比子结点小,所以是最小堆。
但,注意,堆只是约束了父子结点,并没有约束兄弟结点、无关结点的大小,也即是说,除父子结点外,其它结点之间的大小无法确定。比如,下面的最小堆,只能保证根结点是最小的,并不能确定第二小的结点是哪个,第三小的结点是哪个(不过,可以保证,第二小的要么是根结点的左儿子,要么是根结点的右儿子,因为子树是最小堆,子子树也是最小堆)。
堆的初始化
很明显的,上面的完全二叉树根结点要么是最大的,要么是最小的,而且父子结点间有次序,那么是否可以应用于排序?
查找最小值(最大值)
假如有7个数:7 4 2 5 6 3 1,请找出最小的数。
直观的做法是使用擂台法(选其中一个数作为最小数放到擂台,剩余的数依次和擂台上的值比较,更小的留在擂台,最后留在擂台的就是最小值)。
int a[] = {7, 4, 2, 5, 6, 3, 1};
int length = sizeof(a)/sizeof(a[0]);
int min = a[0];
for (int i = 1; i < length; ++i)
{
if (a[i] < min)
{
min = a[i];
}
}
// without test
这种算法从头到尾扫一遍数组,执行了6次比较,所以时间复杂度是O(6),即O(N-1),即O(N)的时间复杂度。
还可以使用冒泡法
int a[] = {7, 4, 2, 5, 6, 3, 1};
int length = sizeof(a)/sizeof(a[0]);
for (int l = length-2, r = length-1; l >= 0; --l, --r)
{
if (a[l] >= a[r])
{
a[l] = a[l] ^ a[r]; // 经典的异或交换算法
a[r] = a[l] ^ a[r];
a[l] = a[l] ^ a[r];
}
}
// without test
冒泡法也要执行N-1次比较。
下面看一下最小堆,上面的数组:7 4 2 5 6 3 1 转换为完全二叉树,结果如下图
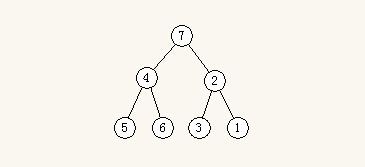
要找到最小的数,将完全二叉树转换为最小堆,那么根结点就是最小的数。
上面的二叉树,需要比较5/6=5 5/4=4 不换, 3/1=1 1/2=1 换, 4/1=1 1/7=1 换共6次才能完成得到最小值。可见,找最小值,堆排序的时间复杂度和上面的擂台法时间复杂度都是O(N)。
注:5/6=5 5/4=4 不换 表示兄弟结点5、6比较,然后和父结点4比较,结果为不需交换的意思
然而,得到最小值后,堆还不是最小堆!!,因为上面交换下来的值,需要逐层下沉,就像上面的结点1与结点7交换了,结点7还需要和下面的儿子结点2、结点3比较,继续下沉。上面没有处理继续下沉的情况,因为求最小值不需要继续下沉。但是如果要建立最小堆,必须考虑递归下沉的情况,据说,数量少的排序,不适宜使用堆排序,因为最小堆(最大堆)的初次建立要耗费比较多的时间(还未考证)。
从上也可见,找最小值(最大值)至少都要比较N-1次,各种算法没有太明显的优劣,时间复杂度都是O(N)。也即是说,如果只是找最小值(最大值)可以放心使用简单的擂台法。
查找最小的(最大的)N个值
假如有7个数:7 4 2 5 6 3 1,请找出最小的3个数。
擂台法
需要比较:6、5、4共15次。即(N-1)+(N-2)+(N-3)....+(N-n)次。时间复杂度接近O(N*N)。
冒泡法
冒泡法和擂台法一样。
最小堆
需要比较:6+x、2、1共9+x次(x表示建立最小堆需要的未知次数)。时间复杂度没计算。只是简单讨论一下堆排序再次查找的时候为什么会更快。
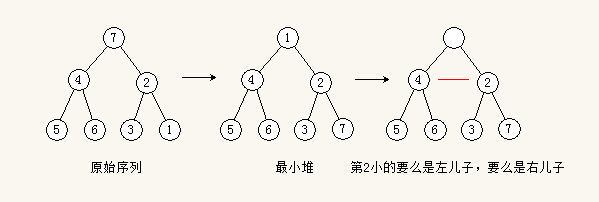
如图,第一次是因为要初始化最小堆,所以需要进行N-1+x次比较,当最小堆建立后,再次查找就能利用最小堆的特性:父结点总比子结点小。所以根结点的左儿子是左子树最小的,根结点的右儿子是右子树最小的。只需要比较这两个儿子,就能确定第2小的数值。也即是说,再次查找最小值,最小堆可以减少比较的次数。
最小堆(最大堆)算法
将一个数组序列转换为最小堆(最大堆)。
主要要点:
- 如果当前结点为
k,那么左儿子为2*k+1,右儿子为2*k+2。 - 先比较两个儿子结点,更小(更大)的才和当前结点比较,这样就能决定哪个儿子需要和当前结点交换。
- 遍历可以从非叶子结点开始,假如结点数为n,那么非叶子结点的数量为
(int)n/2(二叉树,两个结点可以组成一个非叶子结点)。 - 结点的儿子结点不能超出数组下标,超出说明该结点是叶子结点。所以访问儿子结点时,需要先判断儿子的下标是否超出数组长度!!(除非已经确保了不会越界)。
- 进行了交换的结点,需要循环检查到叶子结点,因为可能还需要继续下沉(遇到叶子结点的依据是儿子下标越界)。
- 交换前进行的判断,符号决定了堆是最小堆还是最大堆(更改符号即能从最小堆转换为最大堆)。
下面是一些最小堆的建立算法
int a[] = {7, 4, 2, 5, 6, 3, 1};
int length = sizeof(a)/sizeof(a[0]);
// 从最后一个非叶子结点开始遍历
for (int i = length/2-1; i >= 0; --i)
{
int lchild = i * 2 + 1;
int rchild = lchild + 1;
// 不合法表示是叶子结点,合法表示含有左右儿子
while (rchild < length) { // 循环是因为下沉的结点可能会继续下沉到最后
if (a[i] <= a[lchild] && a[i] <= a[rchild]) {
break;
}
if (a[lchild] <= a[rchild]) { // 左儿子比结点小 (到达这里,说明结点比左、右其中一个儿子大。也即是说,最小的是左、右儿子其中一个
a[lchild] = a[lchild] ^ a[i];
a[i] = a[lchild] ^ a[i];
a[lchild] = a[lchild] ^ a[i];
i = lchild;
} else { // 右儿子比结点小
a[rchild] = a[rchild] ^ a[i];
a[i] = a[rchild] ^ a[i];
a[rchild] = a[rchild] ^ a[i];
i = rchild;
}
lchild = i * 2 + 1;
rchild = lchild + 1;
}
// 不合法表示是叶子结点,合法表示只有左儿子(如果还有右儿子就进入上面了
if (lchild < length)
{
if (a[lchild] < a[i]) { // 左儿子比结点小
a[lchild] = a[lchild] ^ a[i];
a[i] = a[lchild] ^ a[i];
a[lchild] = a[lchild] ^ a[i];
}
}
}
// without test
简化版
int a[] = {7, 4, 2, 5, 6, 3, 1};
int length = sizeof(a)/sizeof(a[0]);
// 从最后一个非叶子结点开始遍历
for (int i = length/2-1; i >= 0; --i)
{
int nth; // 准备下沉的位置
for (int j = i; 2 * j + 1 < length; j = nth) {
// 得到儿子中较大的那个
nth = 2 * j + 1;
if (nth < length - 1 && a[nth + 1] < a[nth]) {
++nth;
}
// 较大的那个和父结点比较
if (a[j] > a[nth]) {
a[nth] = a[nth] ^ a[j];
a[j] = a[nth] ^ a[j];
a[nth] = a[nth] ^ a[j];
// 结点下沉了,需要判断是否需要继续下沉
} else {
break; // 父结点是最小的,不用继续下沉了
}
}
}
// without test
循环下沉
像下面,结点7和结点1交换下沉后,还需要继续和结点2交换下沉。当树更深的时候,下沉还会持续,直到最深的一个叶子结点。
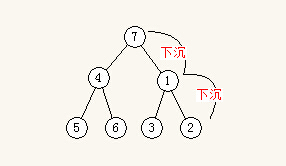
建立堆的过程
其实建立堆的过程,就是对每个结点执行循环下沉,而叶子结点因为不能再下沉了,所以只需要对非叶子结点执行。当对每个结点都进行了循环下沉,最小堆(最大堆)就建立了。
比较与交换
结点、左儿子、右儿子之间的比较,也即是3个数中求最小值(最大值)。
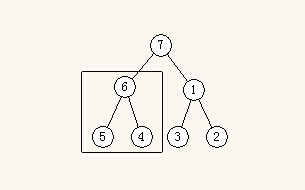
可以知道,N个数中求最小值,至少需要进行N - 1次比较。也即是说,怎样比较,比较的次数都一样。通常习惯的思维是,结点与左儿子比较,结果再与右儿子比较。然而这在代码中并不好做。假如左儿子比结点小,要立即交换吗?不行,因为如果右儿子比左儿子更小,那么就浪费了一次交换。反过来也一样,右儿子比结点小,也不能立即交换。所以,合理的做法是先比较左儿子和右儿子,更小的再和结点比较交换。
为什么自底向上
说到自底向上,有点像冒泡法的感觉。为什么自底向上,最简单的,自底向上可以利用建立好的子堆的特性,减少比较的次数(其实好像比较的次数也没减少到,下沉的时候仍旧需要三个数重新比较)。感觉从上而下也是可以的(从上而下可以比喻成上浮)。
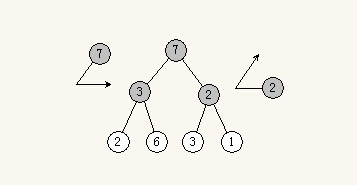
如图,通常是自底向上2 - 3 - 7,感觉7 - 3 - 2也是可以的。
下标问题
for (int i = length/2-1; i >= 0; --i)
是从最后一个非叶子结点遍历到第一个非叶子结点(非叶子结点总数为length/2,遍历下标为0 ~ length/2-1,然后是倒序遍历)。
if (nth < length - 1 && a[nth + 1] < a[nth]) ++nth;
是先判断右儿子是否存在(非叶子结点,说明至少有左儿子),如果右儿子存在,则比较左儿子和右儿子的大小。如果右儿子不存在,那么当前结点要比较的对象是左儿子。
for (int j = i; 2 * j + 1 < length; j = nth)
继续下沉过程,下标与上面的非叶子结点遍历的下标不一样!!而且,继续下沉的过程,仍旧需要判断儿子下标是否出界(因为下沉过程,无法得到子树的非叶子结点数,所以只能循着儿子分支直到遇到叶子结点,遇到叶子结点表示此次下沉已经到底)。
堆排序
上面只是说了堆的建立,要应用到排序还需要进行修改。
通常,堆排序是在建立了最小堆后,将根结点与最后一个元素交换,然后把最后一个元素移除继续调整最小堆,继续交换根结点…以此类推,直到只剩最后一个元素。
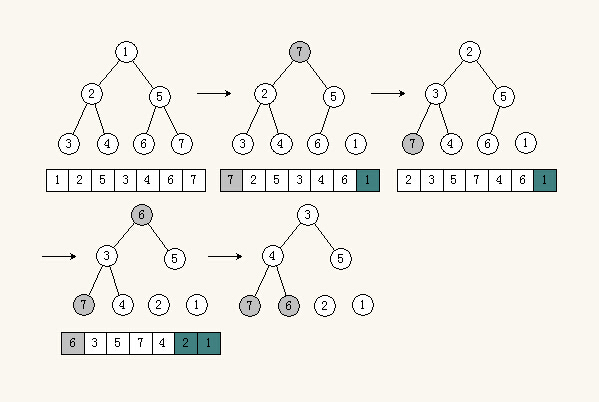
堆排序是不稳定的排序算法。
从上图可以看到:
- 如果建立的是最小堆,那么得到的序列是降序,因为最小的在最后面。
- 反之如果建立的是最大堆,那么得到的序列是升序,因为最大的在最后面。
- 其实无所谓升序降序,因为数组可以从前、后方向遍历。
- 堆排序是不稳定的排序算法。
- 堆顶的元素发生改变,只需要执行一次调整,即一次循环下沉即能复原。
- 堆顶插入元素,先与根结点比较,如果比根结点小则与根结点交换,然后对新的根结点执行下沉(最小堆要比根小,最大堆要比根大)。
堆排序算法代码:
void heap_adjust(int a[], int i, int length)
{
int nth; // 准备下沉的位置
for (int j = i; 2 * j + 1 < length; j = nth) {
// 得到儿子中较大的那个(需要考虑右儿子是否存在)
nth = 2 * j + 1;
if (nth < length - 1 && a[nth + 1] < a[nth]) {
++nth;
}
// 较大的那个和父结点比较
if (a[j] > a[nth]) {
a[nth] = a[nth] ^ a[j];
a[j] = a[nth] ^ a[j];
a[nth] = a[nth] ^ a[j];
// 结点下沉了,需要判断是否需要继续下沉
} else {
break; // 父结点是最小的,不用继续下沉了
}
}
}
void heap_sort(int a[], int length)
{
// 建立最小堆(只是将循环下沉部分抽离)
for (int i = length/2 - 1; i >= 0; --i)
{
heap_adjust(a, i, length);
}
// 第1个元素(i==0)不需要比较
for (int i = length - 1; i > 0; --i)
{
a[i] = a[i] ^ a[0];
a[0] = a[i] ^ a[0];
a[i] = a[i] ^ a[0];
// 最小堆里插入了一个元素,只需要调整一次
heap_adjust(a, 0, i);
}
}
// without test
往最小堆(最大堆)里插入一个元素
往最小堆(最大堆)里插入一个元素,先将该元素与根结点比较,如果比根结点大(小),则该元素与根结点交换,为什么呢,因为堆顶是最小的,如果比堆顶还小,那么即使和堆根交换,也不会影响到堆,堆也不需要调整。所以,只有比堆顶大的时候,才需要交换,这样堆才需要重新调整,重新调整只需要对改变了的根结点执行一次循环下沉即可。
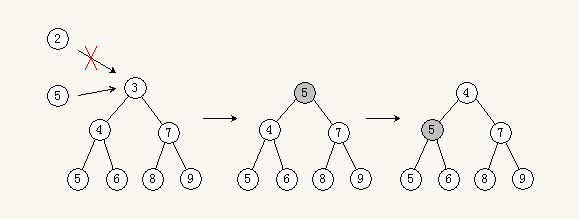
如图,2比最小堆的根3还小,插入是没有意义的,只有比根3大的5插入才有意义。
所以,通常,比最大堆的根还大的无法插入堆,比最小堆的根还小的无法插入堆。
所谓堆排序
观察上面所有的代码,其实建立堆的过程,是对每个非叶子结点执行循环下沉。
如果某个结点发生改变,那么只需要对该结点重新执行循环下沉即可(该结点其实是某个子堆的根结点)。
而循环下沉只对非叶子结点有效,因为叶子结点已经下沉到底了。
上面的算法,使用下沉的思路:
// a[]: 堆 length: 堆的有效长度 element: 要下沉的结点
void sink(int a[], int length, int element)
{
int nth; // 准备下沉的位置
for (int j = element; 2 * j + 1 < length; j = nth) {
// 得到儿子中较大的那个(需要考虑右儿子是否存在)
nth = 2 * j + 1;
if (nth < length - 1 && a[nth + 1] < a[nth]) {
++nth;
}
// 较大的那个和父结点比较
if (a[j] > a[nth]) {
a[nth] = a[nth] ^ a[j];
a[j] = a[nth] ^ a[j];
a[nth] = a[nth] ^ a[j];
// 结点下沉了,需要判断是否需要继续下沉
} else {
break; // 父结点是最小的,不用继续下沉了,整个下沉结束
}
}
}
void heap_sort(int a[], int length)
{
for (int i = length/2 - 1; i >= 0; --i)
{
// 堆的建立,只需要对每个非叶子结点执行下沉(i为非叶子结点的下标)
sink(a, length, i);
}
// 第1个元素(i==0)不需要比较
for (int i = length - 1; i > 0; --i)
{
a[i] = a[i] ^ a[0];
a[0] = a[i] ^ a[0];
a[i] = a[i] ^ a[0];
// 堆的根发生了改变,只需要对根执行一次下沉(根的下标为0)
sink(a, i, 0);
}
}
// without test
测试代码:
#include <stdlib.h>
int main(int argc, char* argv[])
{
int a[] = {7, 4, 2, 5, 6, 3, 1};
int length = sizeof(a)/sizeof(a[0]);
heap_sort(a, length);
for (int i = 0; i < length; ++i)
{
printf("%d\n", a[i]);
}
system("pause");
return 0;
}
时间复杂度与空间复杂度
堆的建立
for (int i = length/2 - 1; i >= 0; --i)
{
// 堆的建立,只需要对每个非叶子结点执行下沉(i为非叶子结点的下标)
sink(a, length, i);
}
堆的建立,需要执行N/2次下沉,下沉算法
下沉算法的时间为要下沉的结点的高度 * 下沉的消耗,从上一篇《完全二叉树》可以知道,结点为N,二叉树最大的高度(树的高度等于深度)为log(2)N,最小堆建立的时候,只需要下沉N/2个结点,而结点的下沉时间取决于结点的高度(注:是高度而不是深度!)。越在下面的结点,高度越低,时间消耗越少。
设树的高度为H,每层的结点数为2^(n - 1),所以:
深度为1,有2^0个结点,需要下沉H - 1高度;
深度为2,有2^1个结点,需要下沉H - 2高度;
深度为3,有2^2个结点,需要下沉H - 3高度;
… …
深度为H - 1(高度为2),有2^(H - 2)个结点,需要下沉1高度。
深度为H(高度为1,有2^(H - 1)个结点,需要下沉0高度(叶子结点)。
所以N个结点,组建最小堆时,需要消耗的总时间为:
S = 2^0*(H - 1) + 2^1*(H - 2) + 2^2*(H - 3) +...+ 2^(H - 2)*1 + 2^(H - 1)*0
简化得S = H + 2H + 4H +...+ 2^(H - 2) - 1 - 4 - 12 - ...
由于结点数为N的树的高度为log(2)N,所以代入上面得S = 2N - 2 -log(2)N,近似O(N)。
说实在的,知道上面的表达式,但是不懂化简,答案是网上搜来的。
所以,堆的建立的时间复杂度为O(N),由于堆的建立是在堆自身的空间上进行的,辅助变量也是常数,所以,堆的建立的空间复杂度为O(1)。
堆排序
堆排序分为两部分,第一步为建立堆,第二步为调整堆。堆排序过程,执行了一次建立堆,每排序一个元素需要执行一次堆调整,所以所有元素排序完成,需要执行N - 1次调整堆。
所以,堆排序的时间复杂度为O(N)+O(log(2)N * (N - 1)),近似O(Nlog(2)N)。
所以,堆排序的时间复杂度为O(Nlog(2)N),由于堆的建立和调整都是在堆自身的空间上进行的,不需要开辟额外的辅助空间,所以,堆排序的空间复杂度为O(1)。
堆排序的应用
堆排序最直接的应用是用来排序。
优先队列
优先队列是指支持插入元素和查找最小(最大)的元素的数据结构。如果使用普通队列来实现这两个功能,那么查找最小(最大)元素需要枚举整个队列,这样的时间复杂度比较高;如果已经排序好的数组,插入一个元素则需要移动很多元素,时间复杂度仍然比较高。而使用堆来实现优先队列,插入元素时无需移动太多元素,查找元素也很轻易找到最小(最大)的那个,所以可以很好解决这两种操作。
查找第n小(大)的数
要查找第n小的数,建立一个大小为n的最大堆,堆顶即为第n小的数。
为什么第n小的数建立的是最大堆
先假设建立的是最小堆,堆的大小为n,那么所有元素插入最小堆后,最小堆里最大的就是第n小的数。然而要得到这个第n小的数,还需要对最小堆进行一次排序,或者要考虑从最小堆里找到最大的数值。
反过来,如果建立的是最大堆,堆的大小为n,那么所有元素插入最大堆后,最大堆里的根是第n小的吗?是的。
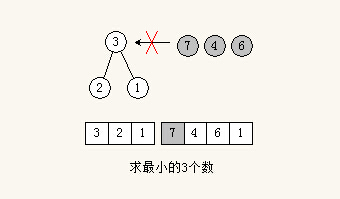
如图,求最小的3个数,先将头3个数构建成最大堆,然后遍历剩余的数。比根结点大,入不了堆;比根结点小,才能入堆;如果入堆了,需要重新调整最大堆。当元素遍历完,最大堆里的数就是最小的3个数,而根结点是第3小的数。
同理,如果要查找第n大的数,需要构建最小堆。
简单理解,把最小的n个数构建成最大堆,根结点就是第n小;同理,把最大的n个数构建成最小堆,根结点就是第n大。
查找最小(最大)的n个数
要查找最小的n个数,建立一个大小为n的最大堆,堆里面的元素就是最小的n个数。同理,如果要查找最大的n个数,建立一个大小为n的最小堆,堆里面的元素就是最大的n个数。
上面求第n小(大)的数最终得到的最大堆(最小堆)就是要查找的最小(最大)的n个数。
学习笔记,仅供参考

